Определение гранулометрического состава и закона распределения размеров частиц помолотого сильвинита |
|
Авторы: В.П. Муленков (группа компаний «Возрождение»), УДК 539.215.2 Экспериментальным методом ситового анализа исследован гранулометрический состав помолотого сильвинита, сырья для получения калийных удобрений. Проведена оценка совокупности размеров частиц сильвинита с использованием теории вероятности и математической статистики, определен закон распределения размеров частиц. В производстве калийных удобрений ОАО «Сильвинит» г. Соликамска используется помол сильвинитовой руды Верхнекамского месторождения. Добытую в шахте руду измельчают в 2 этапа: вначале размельчают в дробилках, затем в мельницах мокрого помола. Размеры получаемых частиц находятся в пределах 0...3,5 мм. Помол частиц является сырьем при получении калийных удобрений методом пенной флотации [1]. Непременным условием эффективности флотации являются размеры частиц сырья, его гранулометрический состав, оптимальность параметров технологического процесса. При исследовании гранулометрического состава помолотого сильвинита применен метод ситового анализа. Сырье просеивалось поочередно на ситах с различными размерами ячеек. Базовая масса, использованная в эксперименте, составляла 9 кг, ее разделили на 3 части по 3 кг. Навески порций насыпаемые в сита составляли 300...350 г, длительность просева порций регламентировали по времени в пределах 4...5 мин. Это позволило получать сопоставимые и достоверные результаты. В процессе эксперимента состав разделили на 11 фракций, каждая из которых в дальнейшем была взвешена, а затем доля каждой фракции посчитана по формуле Сфр = mi/mб*100% (1) Таблица 1 Гранулометрический состав помола сильвинита
Анализ данных табл. 1 показывает что основу смеси составляют 5 фракций: +0,45 -0,63; +0,63 -0,8; +0,8 -1,0; +1,0 -1,25; +1,25 -1,6 мм; на них приходится примерно 76% массы сырья. Три центральных фракции: +0,63 -0,8; +0,8 -1,0; +1,0 -1,25 мм составляют около 50% всей массы помолотого сильвинита. Наибольшая массовая доля приходится на фракцию +0,8 -1,0 мм, она составляет 17%. Вторым этапом экспериментальных исследований было определение массы частиц в отдельных фракциях. Методика эксперимента основана на статистическом подходе и заключалась в следующем. За счет объединения некоторых фракций составили 5 групп: +0,45 -0,63; +0,63 -1,0; +1,0 -1,6; +1,6 -2,0; +2,0 -2,8 мм. Из каждой группы случайным образом отобрали по 1000 частиц, взвешиванием определили массы этих выборок, а затем сосчитали массу 1 среднестатистической частицы для каждой группы. Результаты эксперимента приведены в табл. 2. Таблица 2 Массы частиц средних фракций
Полученные данные необходимы при моделировании технологического процесса флотации калийных солей. Математическая модель, описывающая этот процесс, включает, как один из параметров, массы частиц разных фракций, их кинетическую энергию. Перейдем к статистической оценке исследованного состава помола сильвинита. Вся совокупность значений размеров частиц находится в диапазоне 0...3,5 мм, при этом каждая из частиц имеет отличный от других размер. Эти размеры представляют собой случайные величины. Обозначим возможные значения случайной величины di. Совокупность возможных значений di и соответствующих им вероятностей рi составляют распределение случайной величины. Анализируя рассматриваемое распределение (табл. 1), отметим следующее: - область распределения находится в границах 0<d<3,5 мм; - распределение имеет «шах» в интервале 0,7...0,9 мм; - с увеличением d от 0 до 0,8...1,0 мм плотность распределения случайной величины увеличивается от 0 до «max», а далее, с увеличением d до 3,5 мм, плавно уменьшается, приближаясь к «0»; - характер распределения не указывает на какую-либо близость к симметрии. Отмеченные признаки характерны для логарифмически нормального распределения [2], поэтому рассмотрим исследуемую случайную величину с позиции соответствия этому закону. Поскольку разбивка на интервалы фракций была неравномерной, определялась размерами ячеек стандартных сит, то первоначально приведем эти интервалы к единому интервалу, используя формулу pi=wi/Δdi, (2) где pi - плотность вероятностей распределения размера частиц (1/мм); wi - частота, выраженная в долевом отношении; Δdi - размер «i» интервала. Результаты расчетов приведены в табл. 3. Таблица 3 Плотность вероятностей распределения размеров частиц
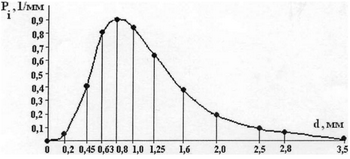
Графическое изображение плотности вероятностей распределения размеров частиц показано на рис. 1.
Рис. 1. Плотность вероятностей распределения размеров частиц помола сильвинита. Форма кривой на рис. 1 подтверждает предположение о логарифмически нормальном распределении. Как для всякого закона распределения случайной величины, для него должно выполняться условие: площадь под кривой линией равняется «1». S = Σ Si, (3) где Si - площадь «i» участка. Графическое построение и расчет по формуле (3) это равенство подтверждает. Логарифмически нормальное распределение формулируется следующим образом: случайная величина подчиняется логарифмически нормальному распределению, если ее логарифм имеет нормальное распределение [3]. Применим этот подход для исследуемых частиц сильвинита. Прологарифмируем случайную величину - размер частицы «d». Для удобства расчета сделаем это через равные интервалы по логарифмической шкале. Результаты логарифмирования приведены в табл. 4. Здесь же показаны соответствующие им экспериментальные значения плотности вероятностей pi. Таблица 4 Исходные данные для расчетов
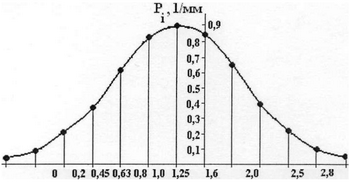
На рис. 2 это распределение показано в графической форме.
Рис. 2.Распределение логарифма размера частиц Экспериментальная кривая, ее характерные признаки позволяют сделать предположение о нормальном распределении случайной величины x = lgd. Закон нормального распределения выражается формулой f(x)=1/(σ*√2П) * exp(-(x-μ)2/2σ2), (4) где σ и μ - параметры распределения (σ - среднее квадратичное отклонение; μ - математическое ожидание). Параметры нормального распределения можно определить непосредственно из графика и расчетом по формулам (5, 6). μ = 1/n * Σxi, (5) σ2 = Σ(xi-μ)2*pi, (6) где xi = lgdi - логарифм размера частиц; рi - плотность вероятностей распределения размера частиц; i - порядковый номер интервала; n - общее число интервалов. Из графика экспериментального распределения плотности (рис. 2) следует, что математическое ожидание μ = 0,1; что соответствует «max» плотности распределения f(х) = 0,9 при х = -0,1. Подставим эти значения в формулу (4) f(x=-0,1) = 1/(σ*√2П) * exp(-(-0,1+0,1)2/2σ2) = 1/(σ*2.5) = 0,9; отсюда σ = 1/(0,9*2,5) = 0,44. Определим также параметры μ и σ по выше приведенным формулам (5, 6), подставляя значение xi, pi из табл. 4. В результате расчетов получено: μ = -0,1 и σ = 0,51. Примем средние значения μ = -0,1 и σ = 0,47 и определим расчетные значения плотности распределения случайной величины х по формуле (4). Полученные результаты, в сравнении с экспериментальными данными, приведены в табл. 5. Таблица 5 Результаты расчета плотности распределения по формуле (4)
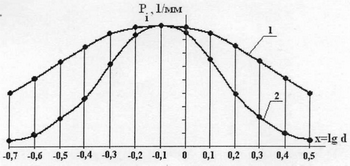
Теоретическая и экспериментальная кривые распределения случайной величины х показаны на рис. 3.
Рис. З. Графики распределения x=lgd: Как следует из графика (рис. 3), теоретические результаты значительно выше соответствующих экспериментальных данных. Сравнение кривых 1 и 2 указывает на качественное сходство расчетных и экспериментальных данных, но значительное их количественное расхождение. Следовательно, исследуемое распределение не соответствует в полной мере нормальному закону. Возьмем формулу (4) за основу и скорректируем ее так, чтобы «ветви» теоретической кривой 1 на рис. 3 приблизились к экспериментальным «ветвям» кривой 2. Параметры μ и σ изменять не следует, так как они получены на основе экспериментальных данных. Имеется только одна возможность - изменить коэффициент при σ2. Очевидно, чтобы «опустить ветви» кривой 1, нужно коэффициент уменьшить. Просчетом нескольких значений получена оптимальная величина коэффициента «0,5». Скорректированная формула (4) принимает вид f(x)=1/(σ*√2П) * exp(-(x-μ)2/0,5σ2), (7) Результаты расчетов по формуле (7) приведены в табл. 6, здесь же для сравнения указаны экспериментальные данные. Таблица 6 Итоговые результаты исследований
Результаты, полученные расчетом по формуле (7) полностью соответствуют экспериментальным данным, что подтверждает правильность корректировки основной формулы (4). Отличие полученного выражения (7) от классической формулы (4) не позволяет считать рассмотренное распределение нормальным, а с учетом того, что в качестве случайной величины взят ее логарифм, то и логарифмически нормальным это распределение считать нельзя. Некоторое несоответствие распределения размера частиц помола сильвинита логарифмически нормальному закону вполне объяснимо. Известна работа академика А.Н. Колмогорова [4], касающаяся распределения размеров частиц породы при дроблении. В ней автор доказывает теоретически, что при последовательном механическом дроблении частиц в пределе, т.е. при неограниченной продолжительности дробления, распределение размеров этих частиц, как случайных величин, соответствует логарифмически нормальному закону. При этом логарифмы размеров частиц имеют нормальный закон распределения. В нашем случае частицы сильвинита получены при ограниченном времени дробления, регламентированным технологическим процессом получения калийных удобрений. Этим, очевидно, и объясняется некоторое несоответствие полученного распределения логарифмически нормальному закону.Таким образом, в результате исследований определен гранулометрический состав помолотого сильвинита - сырья для получения калийных удобрений; подобрана формула для расчета плотности вероятностей распределения частиц, определены, параметры распределения. Полученные данные позволят улучшить технологический процесс флотации калийных удобрений.
Библиографический список 1. Кашкаров О.Д., Соколов И.Д. Технология калийных удобрений. - Л.: Химия, 1978. - 248 с. |





 Определение гранулометрического состава и закона распределения размеров частиц помолотого сильвинита
Определение гранулометрического состава и закона распределения размеров частиц помолотого сильвинита